Motion planning with viability filtering This work looks at exploiting knowledge of agent's viability to expedite motion planning. It was presented at the International Conference on Robotics and Automation 2007, in Rome, Italy, in mid-April 2007. (paper PDF; slides from the talk: PDF) Paper abstract Current motion planners, in general, can neither "see" the world around them, nor learn from experience. That is, their reliance on collision tests as the only means of sensing the environment yields a tactile, myopic perception of the world. Such short-sightedness greatly limits any potential for detection, learning, or reasoning about frequently encountered situations. As a result, it is common for current planners to solve and re-solve the same general scenarios over and over, each time none the wiser. We thus propose a general approach for motion planning, as well as a specific illustrative algorithm, in which local sensory information, in conjunction with prior accumulated experience, are exploited to improve planner performance. Our approach relies on learning viability models for the agent's "perceptual space", and the use thereof to direct planning effort. Experiments with three test agents show significant speedups and skill-transfer between environments.

As a result of viability filtering (right), the planner's search tree contains only viable trajectories.

Basic premise

The basic premise of this work is that, in most cases, exploring nonviable states is a waste of time during motion planning. Nonviable states are ones in which the agent has passed a "point of no return", where collision did not yet occur but is now unavoidable. The only time exploring nonviable states makes sense is if the goal state is itself nonviable, and even then one usually only needs to explore nonviable states in a limited neighbourhood around the goal; in all other cases exploring nonviable states is wasteful because such nonviable states are guaranteed to never contribute to a solution (i.e., to lead to a viable goal state).

A motion planner with viability filtering thus first derives a model of agent's viability, and then simply curtails any tree branches which the model predicts to be nonviable. It is useful to derive viability models which are not strictly tied down to particular environments. To this end one can derive local viability models, which describe the agent's viability in terms of surrounding features and obstacles, rather than in terms of global coordinates. This can be achieved by outfitting the agent with virtual sensors that measure the distance through free-space to the nearest obstacle along particular paths (usually straight lines). By parametrizing viability in terms of these parameters one obtains a model which is applicable to many environments other than the one on which the model was trained; the applicability can be further extended by training the model on a number of disparate environments.

Experiments

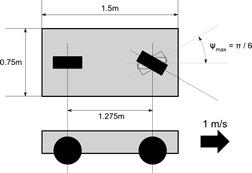
A test implementation was done using RRT-Blossom as the base algorithm to which viability filtering is added. Tests were performed using three agents: an inertial point, a car with limited turning capabilities, and a bike:

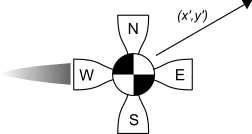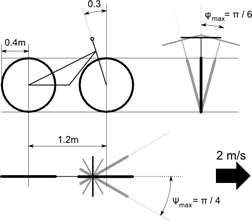Virtual sensors used for the agents:

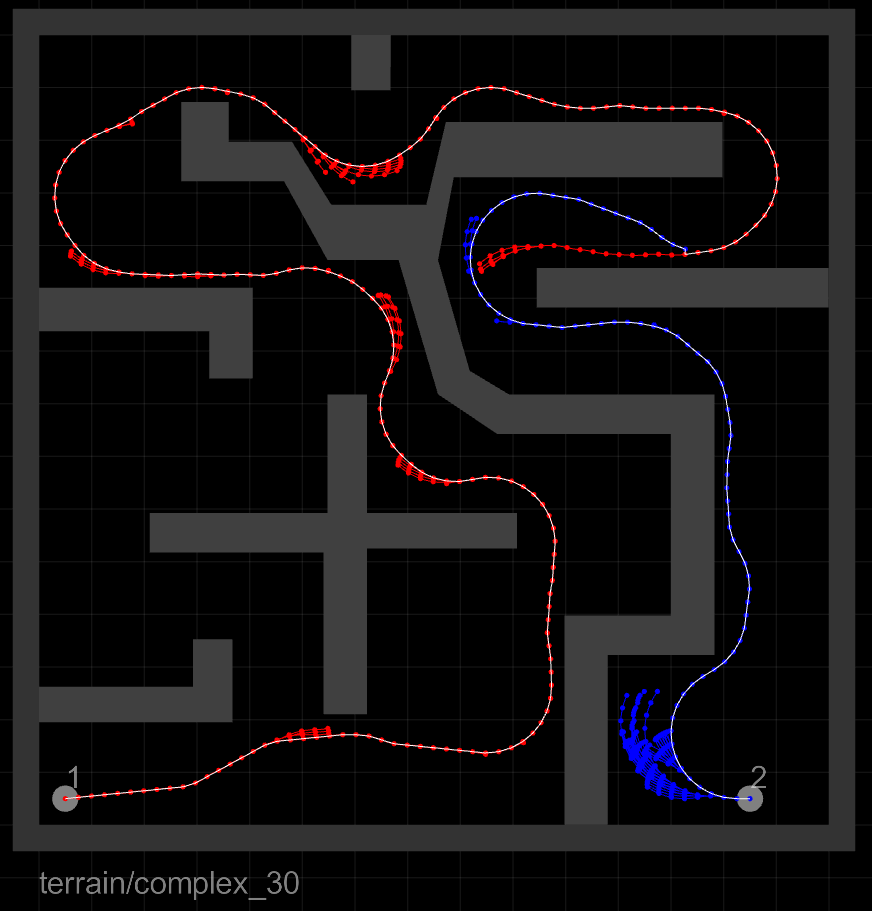
Test environments/problems (the left and right 'X's indicate the starting and goal states, respectively):

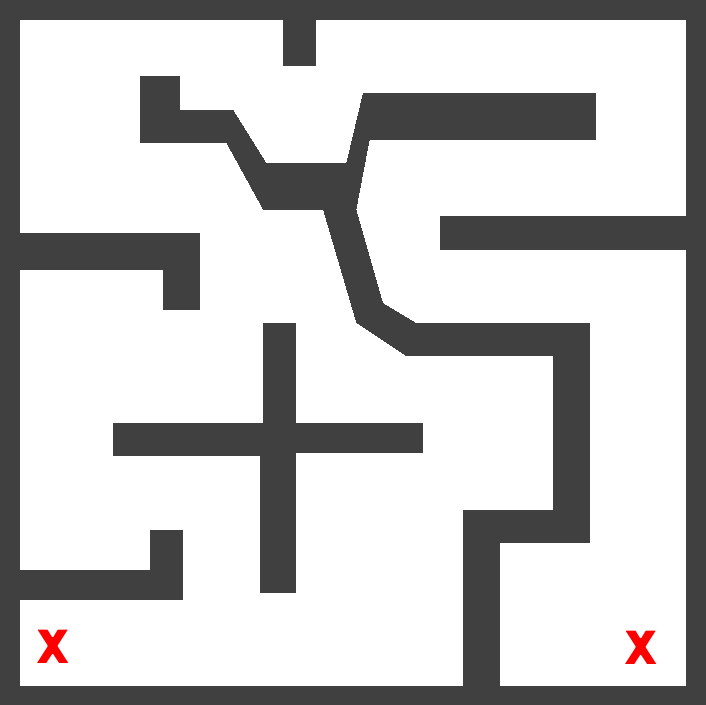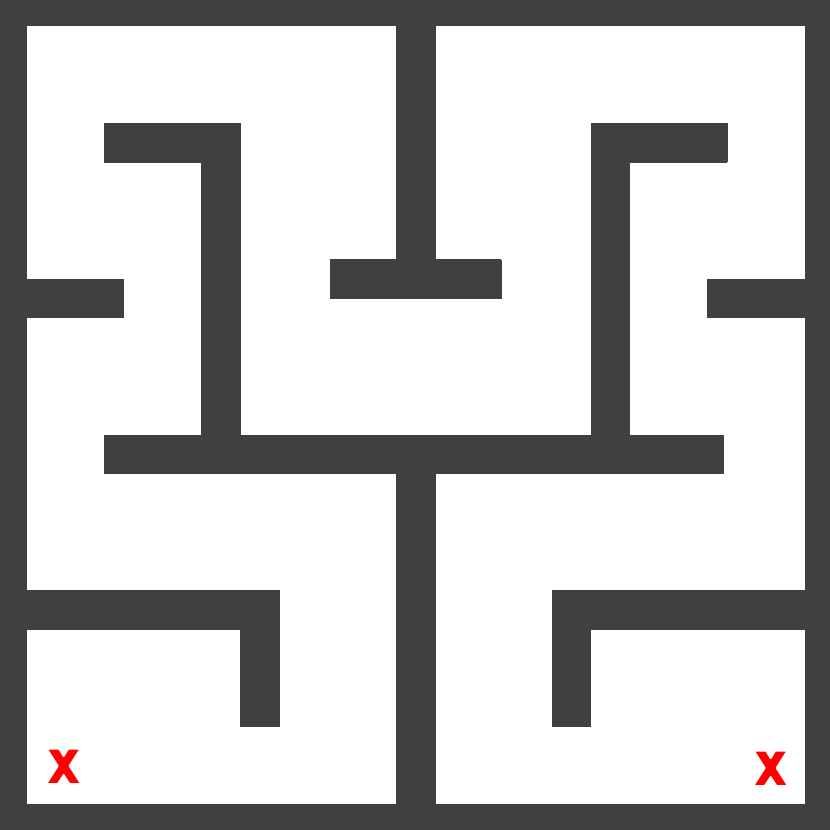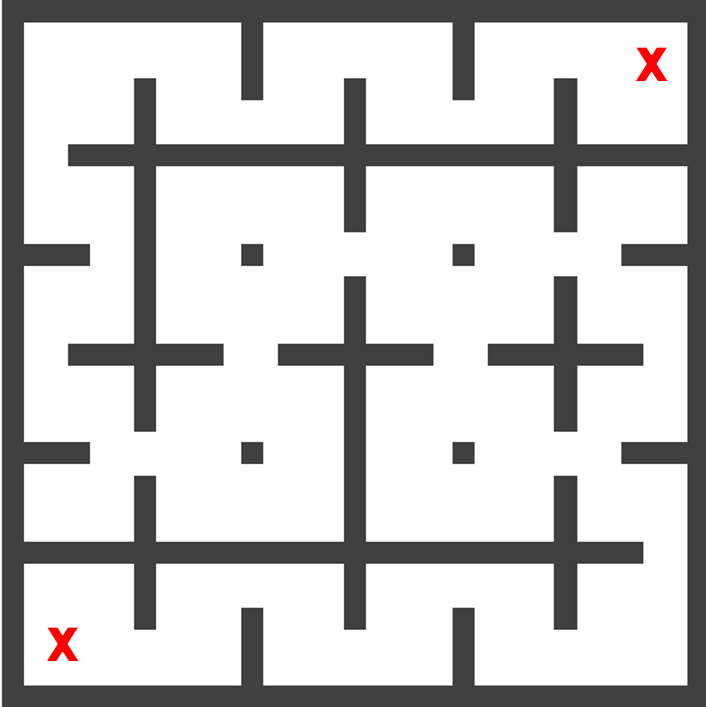complex (native)	Y	IKEA

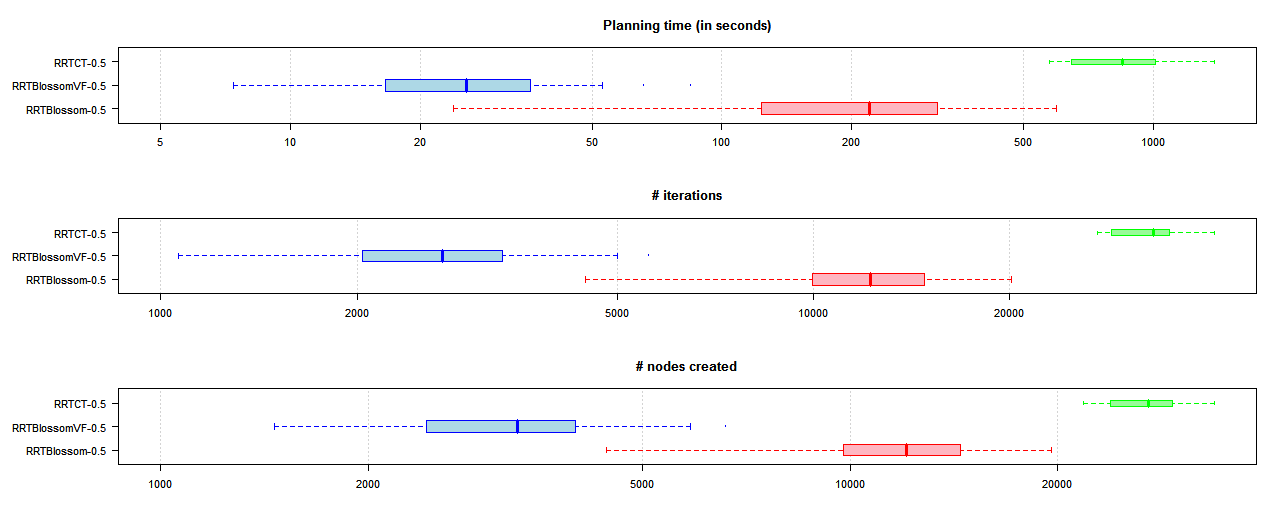
The results show significant speed ups, even despite the extra cost of computing virtual sensor values and querying the viability model. In our experiments we were able to get an order of magnitude improvement over RRT-Blossom in many cases, and sometimes two orders of magnitude over RRT with Collision Tendency (tracking). Speed improvement over plain dual-tree RRT would likely also be at least two orders of magnitude or more, but no data was collected due to the excessively long query times. Below is a boxplot comparing runtimes, number of iterations taken, and number of nodes created for the inertial point agent:

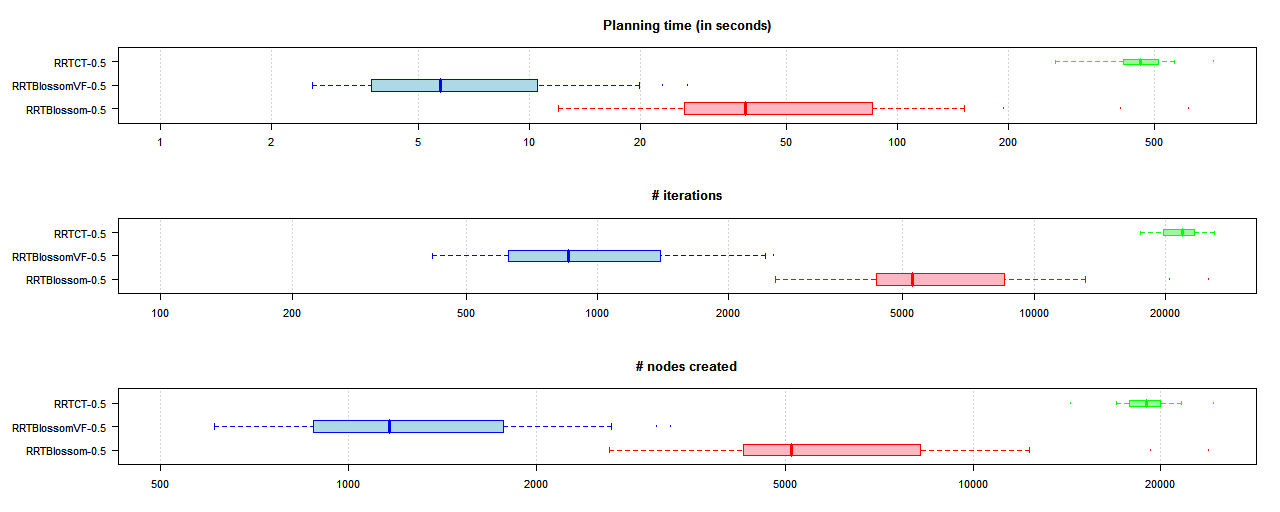
The boxplot in blue indicates the results for the proposed method (i.e., RRT-Blossom with Viability Filtering). Each boxplot summarizes a set of values by drawing a box between the first and third quartile of the values, and extending "whiskers" to samples up to 1.5 times the inter-quartile range. The vertical line through the box indicates the median value, while dots past the whiskers indicate "outliers".

The above plot showed inertial point results in the "native" environment, the one that was used to train the viability model for the agent. Below is the boxplot chart for results for the inertial point in a differente environment but using the same models (thus demonstrating that the models are transferable):

The following tables give numerical results:

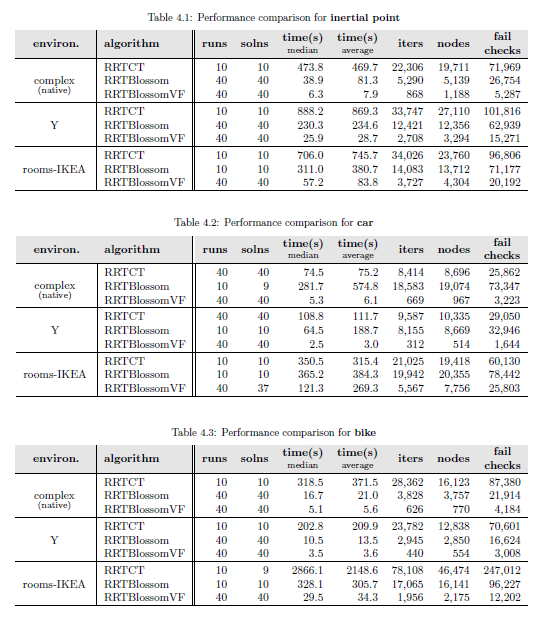
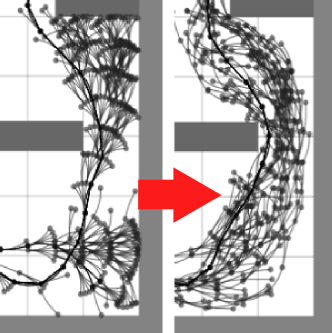
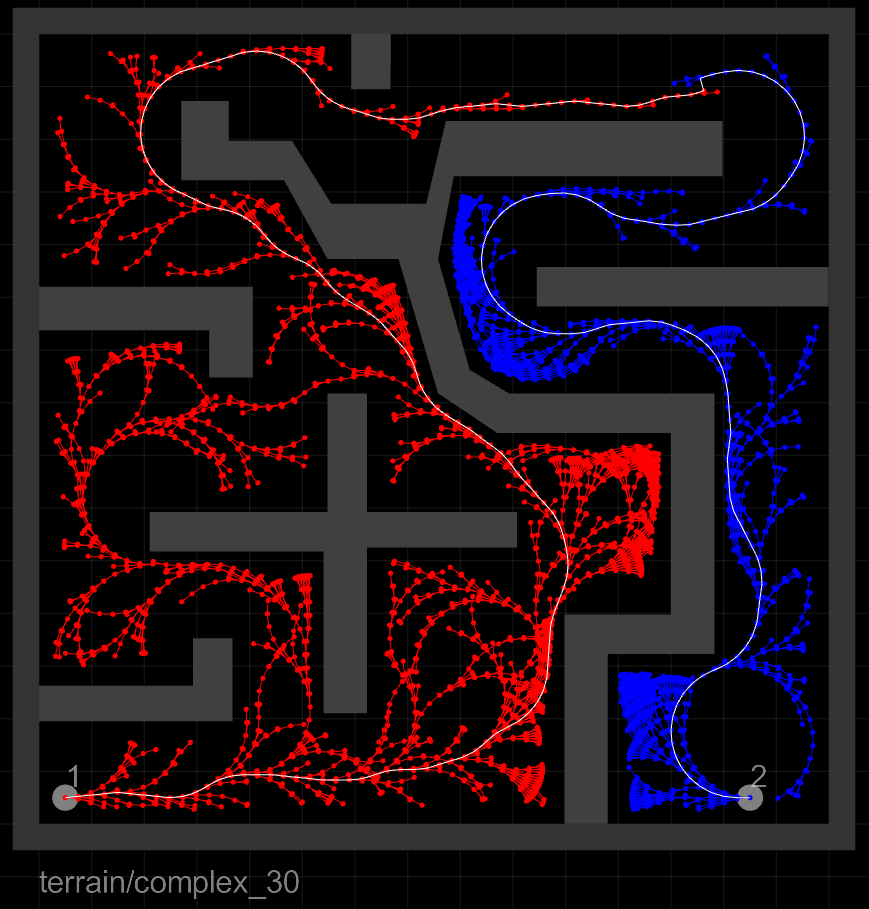
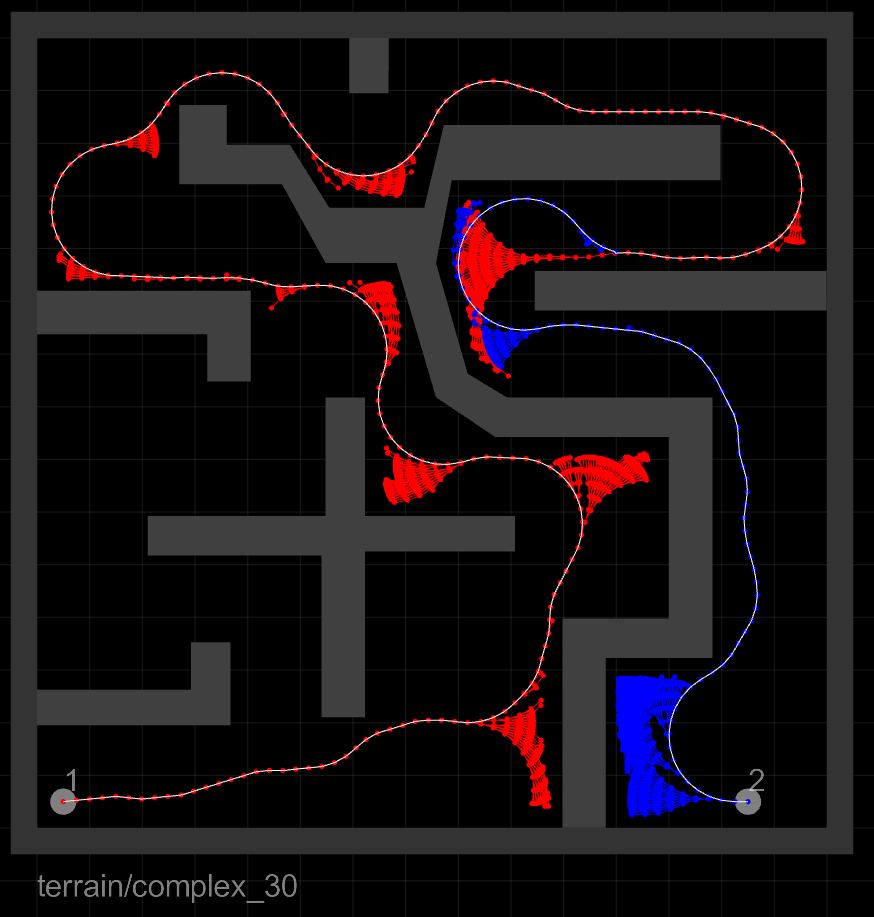
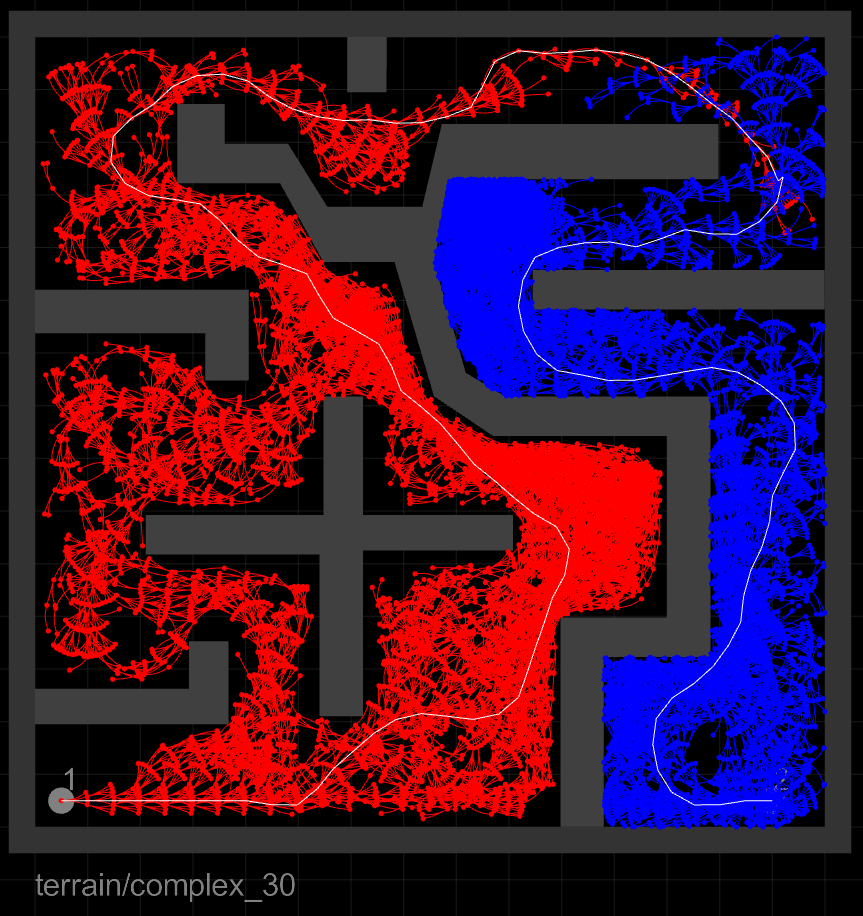
The resultant tree structures also show a markedly reduced number of tree edges needed to find a solution:

	RRT w/Collision Tendency	RRT-Blossom	RRT-Blossom w/Viability Filtering
inertial point
car
bike

The rows, from top to bottom, correspond to the three agents: the inertial point, the car, and the bike. The columns, from left to right, correspond to the three algorithms compared: RRTCT, RRT-Blossom, and RRT-Blossom with Viability Filtering, respectively.

(potential) FAQs

Many thanks to Thierry Fraichard and others with whom I chatted about this and related work after my presentation at ICRA'07, and who have brought up interesting points. Here, as a result, are some potential FAQs:

How is this work related to work on Inevitable Collision States (ICS)?

Both works deal with the same concept, viability, although they address different sides of the coin. The primary focus of viability filtering is purely to make motion planners more efficient and thus speedier; ICS is intended more for ensuring safety of physical agents and robots during motion planning, especially in the face of dynamic and incompletely known environments.

But viability filtering is not even probabilistically complete!

This is true. Theoretically, it should be possible to adapt the viability filtering approach to make it probabilistically complete, but in doing so it would lose some of its power. A much preferable solution we think is to run viability filtering enabled planner in parallel with a provably complete planner. That way, should the viability filtering planner fail to return a solution, one will be returned by the complete planner; should it succeed, we will have obtained a solution in a much shorter time. Such a composite planner would thus be complete, and its average runtime would be significantly faster than that of the original complete planner by itself. In a way, this mimics the human approach to many problems, where simpler and faster approaches are tried first, before resorting to slower, more brute force methods for solving problems.

It is also worth mentioning that in all of our experiments, even with the fairly constrained environments, not once did the incompleteness cause problems (i.e., solutions were found for all queries, given sufficient time).

Is the viability model conservative?

No. On the average there will be equal number of false positives as false negatives.

Isn't this a problem?

If the model were to be used for ensuring agent safety, then clearly this is detrimental, as there is no guarantee of safety. With our focus on faster motion planning, this is not so much a problem. False positives (i.e. nonviable state labelled as viable) are not really a problem, they mere detract from the efficiency of the approach; the error will be caught by a collision-checks on that state's progeny. False negatives (i.e., viable state labelled as nonviable) could potentially cause problems, in that whole solution-critical bottlenecks in the search-space could be erroneously misclassified as nonviable, effectively blocking passage and preventing any solutions. Again, we had no such incidents in any of our tests, which makes us suspect that the bottlenecks would have to be particularly narrow (i.e., nearly air-tight) to produce such effects. See our proposed solution above to such incomplete behaviour.

What about dynamic environments?

The current implementation of viability filtering implicitly assumes a static environment. Interestingly enough, it seems viability theory currently does not seem to support a time-variable constraint set K. Having said that, I think it should be fairly easy to implement using current framework: one simply works in space-time, rather than just space itself. That is, rather than setting K to C_free, the set of collision-free configurations or states, one would instead define K as the set of all collision-free tuples (q,t), where q is the agent's configuration or state at time t. Thus the obstacle space C_obst would morph along the time axis according to the expected/predicted motion of the mobile obstacles. With K so defined, one could then apply the usual viability theorems and method (e.g., Saint-Pierre's computation of a discrete approximation of Viab(K)).

In our case, one additional modification would be needed: the virtual sensors would need to extend through space-time, not just space. That is, the "ray" of the virtual sensor would likewise follow a path through various points (q,t), which in some way approximate the future motion of the agent.

Of course it remains to be seen how practical and effective this would be in a real implementation.

Where can I get more information?

For those interested in the topic, it is worth noting that in a month or so I should be placing online a copy of my PhD dissertation (well, a draft of it), which contains a chapter devoted to just this work, and where much more detail can be found. Of course, until then I will also gladly answer any queries you may have be email.