The transformational operator ![]() will
be extended to further generalize interval arithmetic.
will
be extended to further generalize interval arithmetic.
We envision numbers as a tool used to describe things. Many of the things described by numbers are parameterized. For example, we may be using a number to describe the mass of an iron ball. The iron ball can be parameterized by its radius. We will bring these parameters into our number system. This integration of parameters into numbers will give us hints as to how numbers depend on the parameters. These hints will enable the new interval routines to return much tighter results.
To start, we will consider a number system with a single
parameter ![]() . The parameter can vary from zero to
one, and is a real number. Again, as a starting point
we will consider only linear relationships between
the parameter and the value's bounds. This new number system,
using real numbers as the underlying number system,
is denoted by
. The parameter can vary from zero to
one, and is a real number. Again, as a starting point
we will consider only linear relationships between
the parameter and the value's bounds. This new number system,
using real numbers as the underlying number system,
is denoted by ![]() or
or
![]() . The subscript,
. The subscript, ![]() ,
states that a linear relationship is used;
the greek letter
,
states that a linear relationship is used;
the greek letter ![]() signifies
the parameter
signifies
the parameter ![]() of the linear function,
while the latin letters p and q
signify coefficients of the linear function.
of the linear function,
while the latin letters p and q
signify coefficients of the linear function.
A linear interval is described by a lower and
upper endpoint, each of which is a linear function
of ![]() . The coefficients of the linear functions
must be numbers of the underlying system
. The coefficients of the linear functions
must be numbers of the underlying system ![]() .
.
![]()
The semantics of the interval
![]() is: when parameter
is: when parameter ![]() has value k,
the interval represents a fixed real number between
a+bk and c+dk. This can be stated formally as:
has value k,
the interval represents a fixed real number between
a+bk and c+dk. This can be stated formally as:
![]()
![]()
![]()
![]()
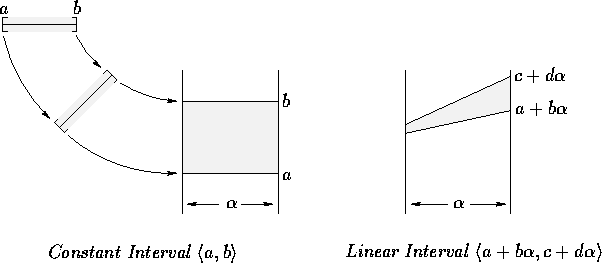
A picture may soothe the intuition.
Associate the interval ![]() with the closed set [a,b], of extended real numbers.
The free variable
with the closed set [a,b], of extended real numbers.
The free variable ![]() may be accommodated by
introducing a new dimension. The interval
may be accommodated by
introducing a new dimension. The interval ![]() does not interact with this new dimension, although
the interval
does not interact with this new dimension, although
the interval ![]() does.
The earlier intervals may now be regarded as ``constant intervals''.
does.
The earlier intervals may now be regarded as ``constant intervals''.
An example is appropriate. Consider the problem
of determining the range of an arbitrary function ![]() over the domain [0,1]. The parameter
over the domain [0,1]. The parameter ![]() in this case is the argument to the function.
The range may be computed by simply evaluating
the function with x being a number
representing the domain of interest, [0,1].
in this case is the argument to the function.
The range may be computed by simply evaluating
the function with x being a number
representing the domain of interest, [0,1].
Since ![]() varies over [0,1], the linear
function
varies over [0,1], the linear
function ![]() represents the domain completely:
every element of the domain [0,1] is represented
by
represents the domain completely:
every element of the domain [0,1] is represented
by ![]() , for some value of
, for some value of ![]() .
It follows that the linear interval
.
It follows that the linear interval ![]() represents the domain: every element of the domain is
contained in the interval
represents the domain: every element of the domain is
contained in the interval ![]() .
The constant interval
.
The constant interval ![]() represents
the domain since every element of the domain
is represented by an element of
represents
the domain since every element of the domain
is represented by an element of ![]() .
.
Consider the simple function g(x) = x - x.
So, with ![]() , this proceeds as follows:
, this proceeds as follows:


The linear real interval number system may be denoted by
![]() . The notation follows
from the denotation
. The notation follows
from the denotation ![]() for the
linear floating point interval number system:
for the
linear floating point interval number system:
![]()
A linear interval model ![]() of an n-ary
function
of an n-ary
function ![]() satistfies the inclusion property if
satistfies the inclusion property if
![]()
![]()
The linear interval extension of the n-ary function g is defined as follows:
![]()
The demotions ![]() and
and ![]() are
significant in the definition of interval extension because there
is no best demotion available. This is drastically different
from the demotions
are
significant in the definition of interval extension because there
is no best demotion available. This is drastically different
from the demotions ![]() and
and ![]() used in
the definition of floating point interval extensions. When demoting
an extended real to a float, there is a particular floating
point number which is the best choice. When rounding down,
the largest floating point number less than or equal to the
extended real is chosen. The best choice when demoting an arbitrary
extended real function l to a linear extended real function
used in
the definition of floating point interval extensions. When demoting
an extended real to a float, there is a particular floating
point number which is the best choice. When rounding down,
the largest floating point number less than or equal to the
extended real is chosen. The best choice when demoting an arbitrary
extended real function l to a linear extended real function ![]() depends on how
depends on how ![]() will be used. This
significantly changes the character of the interval extension.
It can no longer be used to show an interval model is optimal
in general, although it may be used to show that an interval
method is suboptimal.
will be used. This
significantly changes the character of the interval extension.
It can no longer be used to show an interval model is optimal
in general, although it may be used to show that an interval
method is suboptimal.
| Jeff Tupper | March 1996 |