Next: 4.7.5 Hansen's Linear Interval Arithmetic
Up: 4.7 Other Work
Previous: 4.7.3 Extended Interval Arithmetic
When working with interval methods, computed bounds on
derivatives often supplement computed bounds on values.
A simple example problem will illustrate the core technique:
consider bounding the range of g(x), for 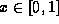 .
In chapter two, we bounded the range of g(x)
by evaluating
.
In chapter two, we bounded the range of g(x)
by evaluating
or
another approach is to evaluate
with 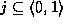 .
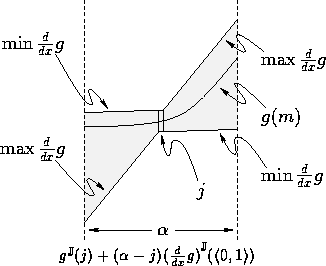
Usually, j is taken to be the midpoint of the domain:
.
Usually, j is taken to be the midpoint of the domain:
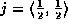 ,
so
bounds g(x) for
,
so
bounds g(x) for 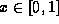 .
The midpoint is chosen, as it often produces the
best bounds possible with this approach.
.
The midpoint is chosen, as it often produces the
best bounds possible with this approach.
This approach, based on the first derivative,
may be graphically depicted, as follows:
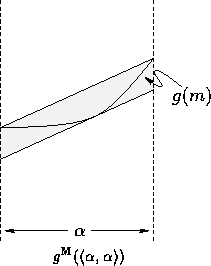
The linear interval approach may be similarly depicted,
as follows:
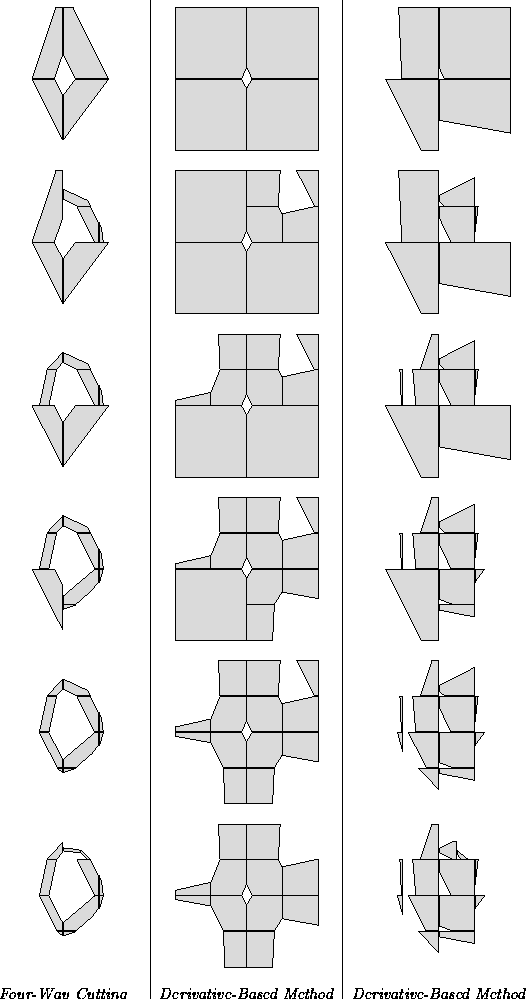
The following diagram depicts renderings of
over 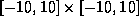 using linear interval arithmetic, and two
derivative-based methods. The linear interval
arithmetic method uses four-way cutting, the
simplest progressive method discussed.
The two derivative-based methods both use
the first derivative only, but differ in their
placement of the sample
using linear interval arithmetic, and two
derivative-based methods. The linear interval
arithmetic method uses four-way cutting, the
simplest progressive method discussed.
The two derivative-based methods both use
the first derivative only, but differ in their
placement of the sample 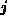 . One places
. One places
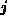 at the center of the cluster;
the other places
at the center of the cluster;
the other places 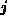 at the bottom left
corner of the cluster.
As each method uses a different number of interval
evaluations per stage, the following diagram does
not indicate the relative efficiencies of the different
methods.
Clearly, the linear interval arithmetic produces
superior intervening renderings, as
fewer spurious visual artifacts are present in the
renderings produced using linear interval arithmetic.
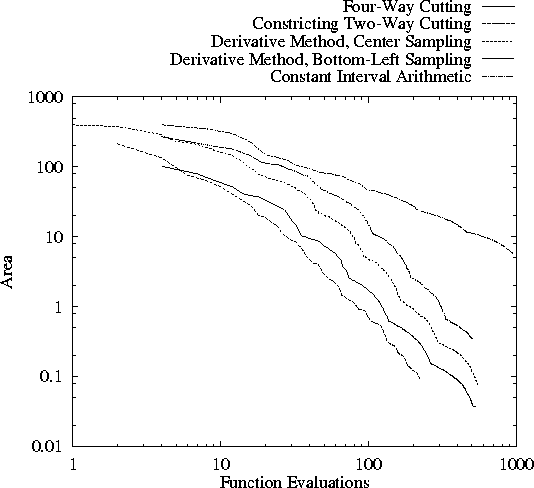
The following diagram illustrates the efficiency
of the various methods when rendering
the aforementioned equation:
Of course, the derivative methods are not
competitive when the underlying
functions are not differentiable.
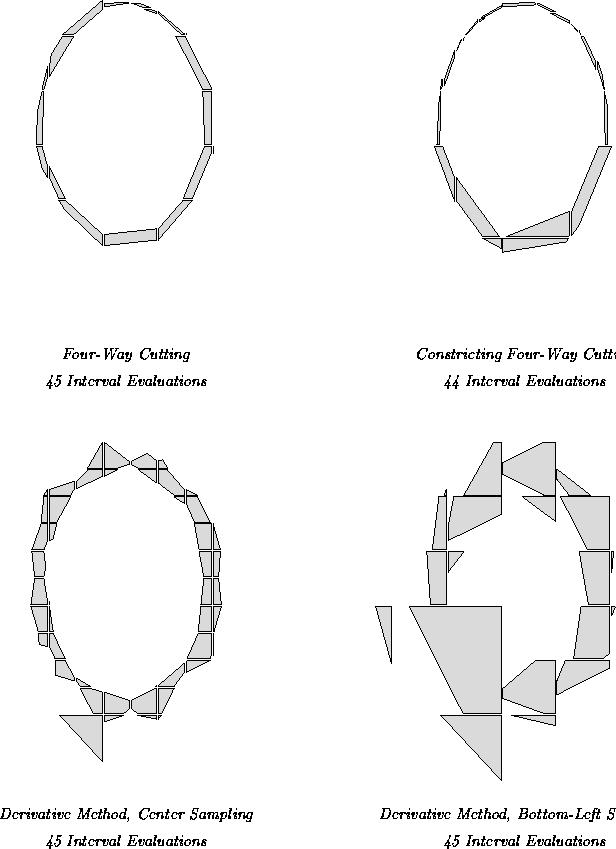
The following diagram illustrates the information
gained, using each method, after 45 interval
evaluations:
An interval arithmetic similar to
at the bottom left
corner of the cluster.
As each method uses a different number of interval
evaluations per stage, the following diagram does
not indicate the relative efficiencies of the different
methods.
Clearly, the linear interval arithmetic produces
superior intervening renderings, as
fewer spurious visual artifacts are present in the
renderings produced using linear interval arithmetic.
The following diagram illustrates the efficiency
of the various methods when rendering
the aforementioned equation:
Of course, the derivative methods are not
competitive when the underlying
functions are not differentiable.
The following diagram illustrates the information
gained, using each method, after 45 interval
evaluations:
An interval arithmetic similar to 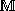 may be implemented using derivative-based methods.
may be implemented using derivative-based methods.
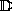 denotes such an arithmetic, which
bounds both the value and first derivative of evaluated
functions. Each element of
denotes such an arithmetic, which
bounds both the value and first derivative of evaluated
functions. Each element of 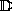 is given
by a first component
is given
by a first component 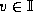 , which bounds the
value at
, which bounds the
value at 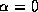 , and a second component
, and a second component 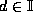 ,
which bounds the derivative for
,
which bounds the derivative for 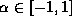 .
Domains other than [0,1] are possible; as are other
sample locations. Further discussion of this approach
can be found in the next subsection.
.
Domains other than [0,1] are possible; as are other
sample locations. Further discussion of this approach
can be found in the next subsection.
Next: 4.7.5 Hansen's Linear Interval Arithmetic
Up: 4.7 Other Work
Previous: 4.7.3 Extended Interval Arithmetic
![]() .
In chapter two, we bounded the range of g(x)
by evaluating
.
In chapter two, we bounded the range of g(x)
by evaluating
![]()
![]()
![]()
![]()
![]()