There is another way to approach evaluating ![]() ,
when g is neither concave up nor concave down.
We consider g such that
,
when g is neither concave up nor concave down.
We consider g such that
![]() .
Restricting our attention to continuous g, we may find
an upper bound without splitting g into two parts.
Consider the following chart, a
.
Restricting our attention to continuous g, we may find
an upper bound without splitting g into two parts.
Consider the following chart, a ![]() chart
where
chart
where ![]() and
and ![]() .
.
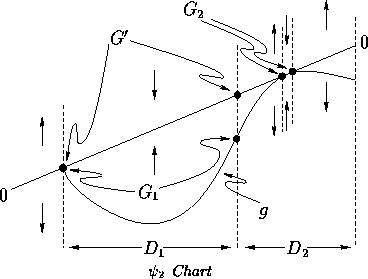
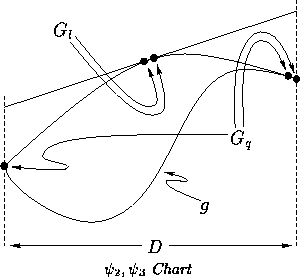
Another approach is to find a quadratic upper bound and then produce
a linear upper bound of the quadratic upper bound.
This may be done if ![]() .
.
| Jeff Tupper | March 1996 |