Next: 1.4 Numerical Round-Off
Up: 1 Motivation
Previous: 1.2 Implicit Equations
Let us turn our attention to a more difficult problem.
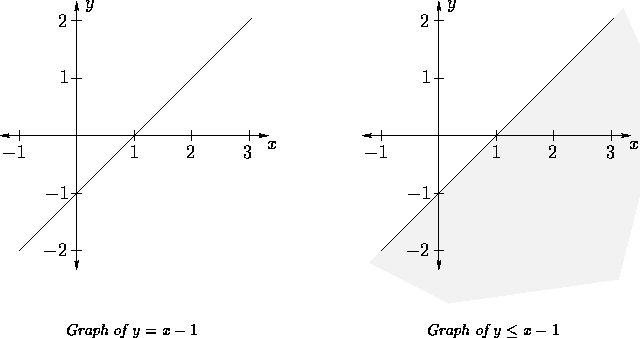
Consider graphing a relation, such as
The procedure taught is to first graph the boundary;
the boundary of 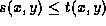 is given by s(x,y) = t(x,y).
Our example's boundary is given by
We then shade in the appropriate side.
is given by s(x,y) = t(x,y).
Our example's boundary is given by
We then shade in the appropriate side.
It may seem that graphing relations is not much harder than graphing
equations, given the simple approach outlined earlier.
But consider the two relations
Both have the same boundary, which does not break the plane nicely
into two ``sides''.
The two relations have different graphs, one of which
may be given by our side-testing procedure.
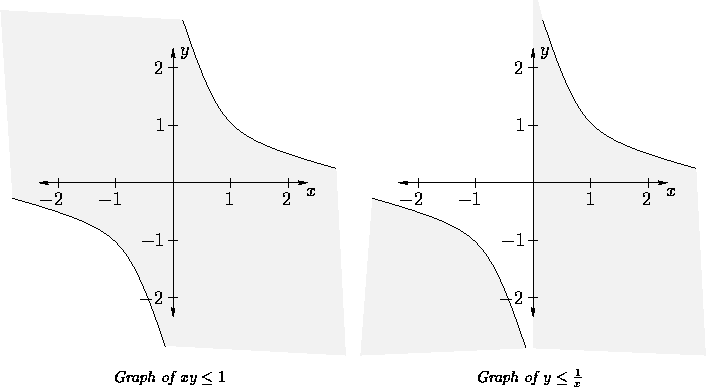
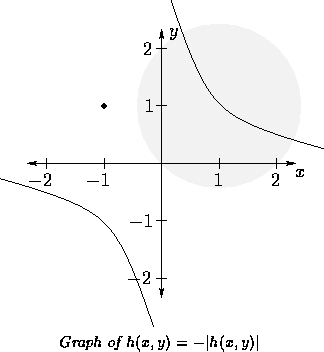
If this is not troubling enough, consider the relation
which, again, has the same boundary as the two
earlier relations xy=1 and 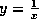 .
The graph of this new relation follows:
The graph contains all points that satisfy
The only true relationship between the boundary
of a graph and the actual graph is that of containment:
the graph contains its boundary. In the case of strict
inequality, the graph does not contain its boundary.
.
The graph of this new relation follows:
The graph contains all points that satisfy
The only true relationship between the boundary
of a graph and the actual graph is that of containment:
the graph contains its boundary. In the case of strict
inequality, the graph does not contain its boundary.
It appears that graphing relations is indeed more difficult than
graphing equations.
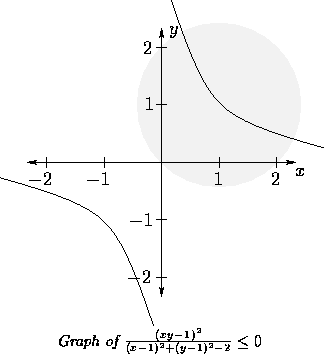
However, this is not the case; consider the following relation:
This relation may be expressed as an equation, as follows:
We have not chosen a simpler problem: we have, however, illustrated
some of its hidden difficulties.
These difficulties are nicely illustrated in the next example.
A single graph may contain zero, one, and two-dimensional elements;
consider the equation
whose graph follows:
The graph contains all point which satisfy
It seems that the entire idea of generating graphs as collections
of lines is fundamentally flawed, as a graph may contain two-dimensional elements.
Representing two-dimensional elements with a collection of lines
is inefficient at best, and simply unconscionable at worst.
Next: 1.4 Numerical Round-Off
Up: 1 Motivation
Previous: 1.2 Implicit Equations
![]()
![]()
![]()
![]()
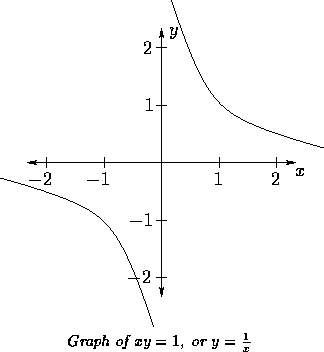
![]()
![]()
![]()
![]()
![]()
![]()